![]()
|
Raymond A.K. Cox is a professor of Finance at Central Michigan University. John B. Mitchell is an Associate Professor of Finance at Central Michigan University. Kee H. Chung is a Professor of Finance at the University of Memphis.
INTRODUCTION
On a daily basis we are being bombarded by "news" describing the lifestyle and exploits of superstars. The "Superstar phenomenon" is where a relatively small number of people dominate the activities in which they are engaged and earn enormous amounts of money, such as Michael Jordan in basketball or Arnold Schwarznegger in movies. Extraordinary incomes earned by superstars may be driven by an allocative equilibrium in which markets reward talented people with increasing returns to ability. Or perhaps, the superstar phenomenon has nothing to do with the differential talent of individuals. For instance, the phenomenon may emerge as a result of certain consumer behavior. If enormous incomes earned by superstars are the markets' reward for their superior talent, the superstar phenomenon may be socially admissible. If, on the other hand, the source of their high incomes is not their talent, the skewness in income distributions caused by the phenomenon may be perceived as inequitable by society. It is the purpose of this paper to explore the existence of the superstar phenomenon in the finance, accounting and economics scholarly publication industry.
Rosen suggests that much of the superstar phenomenon can be explained by convexity of sellers' revenue functions since the convex revenue function implies that the distribution of rewards is more skewed than the distribution of talent (i.e., small differences in talent are magnified into disproportionate levels of success). Rosen shows that the convexity of revenue functions and the extra skew it imparts to the distribution of earnings can be obtained by imperfect substitution (i.e., lesser talent is a poor substitute for greater talent) among different sellers. Rosen also demonstrates that the joint consumption technology (i.e., a performer puts out more or less the same effort in front of audience readerships of ten or one thousand), combined with imperfect substitution, can explain the marked concentration of output on those who have the most talent.
In a similar vein, [MacDonald 1988] presents a dynamic version of Rosen's superstar model. He shows that in equilibrium only the young enter the occupation and earn low incomes playing (writing for small readership audiences) to small crowds, and only the successful stay on. Overall, there are few stars in the industry but as a group they serve a large fraction of the audience and earn an even larger share of the rewards. In order to test the empirical significance of the theory of superstar, [Hamlen 1991] examined the relationship between talent (proxied by voice quality) and success (measured by record sales) in the popular music industry while controlling for other factors such as gender, race, the type of music, and the duration of career. Although empirical results show that consumers recognize quality, the estimated elasticity of record sales with respect to voice quality is less than unity, repudiating the implication of the Rosen-MacDonald theory of superstar.
This paper examines the phenomenon of superstar from a perspective which is significantly different from that of the above studies. Specifically, this study employs a stochastic model of Yule and Simon as the probability mechanism underlying the editor's choice of an author'sarticles and predicts that author's outputs (articles) will be concentrated among a few lucky individuals. We find that the probability distribution implied by the stochastic model provides an excellent description of the empirical data in the publishing of finance, accounting and economics articles. Because the stochastic model does not require differential talents among individuals, our empirical results suggest that the superstar phenomenon could exist among individuals with equal talent. Hence our results are, in spirit, similar to those of Adler.
Another aspect to the superstar phenomenon is where do individuals acquire and practice their talent. Brown (1996) explores, among other things, the institutional source of authors of classical accounting articles as well as their present employer affiliation. That is, where are accounting authors educated (trained) and where do they work? Lukka and Kasanen (1996) study the geographical breadth of accounting knowledge. Their findings suggest that accounting influence is very much localized rather than a global phenomenon.
A STOCHASTIC MODEL OF SUPERSTARDOM
The Rosen-MacDonald theory of superstars centers on an implicit comparison of success relative to the differences in talent. In this section we show that the phenomenon of the superstar does not require differential talents among individuals using the stochastic model of Yule and Simon as a representation of the editor's choice behavior. Simon suggests that a variety of sociological, biological, and economic phenomena are driven by certain probability mechanisms. Specifically, he shows that a wide range of empirical data (e.g., distributions of incomes by size, distributions of cities by population, distributions of biological genera by number of species, and distributions of scientists by number of papers published) conforms well to a class of distributions which can be obtained form stochastic processes similar to those yielding negative binomial of log series distributions. This class of distributions is given by: [Simon, 426]
| f(i) = SB(i,p + 1), | (1) |
where S and p are constants and B (i, p + 1) is the beta function of i and p + 1, i.e.,
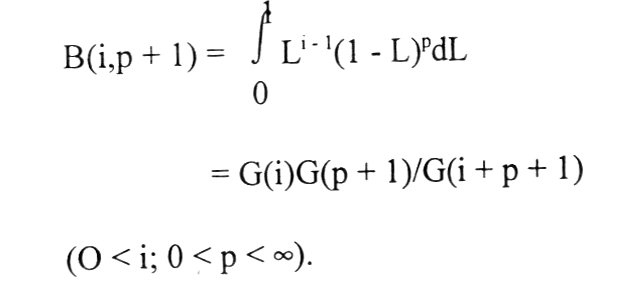 |
(2) |
It is because the class of distributions represented by the expression (1) was first derived by G. Udny Yule, that this distribution carries his name.
In essence, the stochastic process that would lead to the Yule distribution can be characterized as follows. Since the main thrust of this paper is to examine whether the Yule distribution can describe the relative number of finance, accounting or economics articles published by an author, we portray the process in such a context. For simplicity and without loss of generality, suppose that each scholarly journal editor accepts the same number of articles, n, and that the articles are accepted in the following order: All editors first accept sequentially one article each. After the last scholarly journal editor has accepted her first article, the process repeats itself with the second article, and so on. Of course for each editor, articles …article, s,t = 1,2,...,n. Then, the following two assumptions depicting the probability mechanism underlying the editor'schoice of her next article yields the Yule distribution1:
Assumption I: The probability that scholarly journal editor K + 1 accepts an article from an author who was already chosen by exactly i of the K previous editors is proportional to i.
Assumption II: There is a constant probability, D, that scholarly journal editor K + 1 accepts an article from an author who was not yet accepted by any of the previous K editors.
In spirit, the process implied by these assumptions is similar to the superstar generating process suggested by Adler. Adler suggests that the superstar phenomenon exists where consumption requires knowledge. He claims that the need to discuss with other knowledgeable individuals to become familiar with an artist's work (author'sarticle) as a prerequisite to the consumption (acceptance), of the artist's work (author'sarticle) is an essential element in understanding the phenomenon. He argues that consumers (editors) minimize the cost of searching for knowledgeable discussants by choosing the most popular artist (author). Adler suggests that consumers (editors) are better off by patronizing the star (authors) when either other artists (authors) are not cheaper by more than the savings in search costs or other artists (authors) are not sufficiently better than the star (author).
Probability mechanisms underlying the superstar generating process proposed by Adler can be summarized as follows: Suppose that consumers (editors) believe at first that all artists (authors) are equally likely to become stars, and that each consumer (editor) picks one artist (author) at random. Assume further that consumers (editors) live n periods and revise their prior distributions after each period. If there were a slight majority of consumers that select an artist (author) as their choice, that artist (author) would snowball into a star because after each period the majority would increase. In other words, if at any period of time an artist (author) had a market share (number of published articles) only marginally larger than everybody else, this share would increase steadily, and ultimately the artist (author) becomes a star.
That is, even though many journals follow a blind refereed review process, the author'sidentity is known. In the case of single-blind review, the author does not know the reviewers, but the reviewers know the author. A double-blind refereed review process makes the author identity unknown to the reviewers, but the editor still possesses the knowledge. Furthermore, the editor has a great incentive to increase the reputation of their journal by publishing papers written by "star" authors. Thus, the potential for manipulation exists, as the editor is acting in the best interests of the journal. Additionally, some paper acceptances occur because of amiable liaisons and the author identity being known to the editor.
Another factor impacting on the editor's decision to accept or reject the submission of an author's article is the phenomenon of "fishing". Fishing occurs when an author sends their manuscript to a journal with the ex ante strong belief that it will be rejected. Reasons for the submission include:
(1.) Posturing, that is, one can tell your colleagues that your paper is sitting at the desk of some lofty journal, and
(2.) Low cost to obtain reviewer comments used to improve the manuscript, especially done by unknown authors at institutions with reduced research support resources.
The existence of fishing empowers the editor to prescreen author's paper submissions and be inclined to accept star author's papers.
Notice the close proximity between the assumptions underlying the Yule distribution and the superstar model proposed by Adler. It is not clear whether the above assumptions are a realistic representation of the process creating superstars in the finance, accounting and economics scholarly journal article publishing industry. Ultimately, the reasonableness of these assumptions can only be judged by the prescriptive power of their implication, i.e., the Yule distribution. Considering the ubiquity of the distribution in a wide range of social and economic data, however, we conjecture that it may have some predictive content in describing the superstar phenomenon. In the following sections, we examine whether the distribution can describe the cross-sectional distribution of author output, measured by the number of published journal articles.
EMPIRICAL RESULTS
A. Data Description
Data for the present study of finance, accounting and economics are from Heck and Cooley 1988, Chung, Park and Cox 1992 and Cox and Chung 1991, respectively. These sources provide frequency distributions, among other things, of the number of authors with one, two, three and so on, published scholarly journal articles2. Table 1 shows the frequency distributions of authors by the number of journal articles for finance, accounting, and economics.3,4 For finance, among 6,270 authors who published at least one finance article, 3900 authors (62.2%) have one article, 959 authors (15.3%) have two articles, and so on. Likewise accounting has a similar skewed distribution, revealing a high of output concentration among top "star" authors, with 57.7% of authors having published one article, 16.7% having two articles, et cetera. Economics is extremely similar to accounting with 57.7% of authors having one article, 16.4% having two articles, and so on.
B. Empirical Testing
Simon suggests that the Yule distribution provides a good fit to various empirical data, particularly when the value of p is equal to one. Hence, in this paper we assume, as an empirical approximation, that the probability that editor k + 1 accepts a paper which was not yet chosen by any of the previous k editors is small (D . 0), so that p is close to 1 since p = 1/(1 - D). For this case the distribution (1) can be approximated by the following form: [Simon 1955, 426]
| f(i) = 1/i(i + 1), Sf(i) = 1, | (3) |
where f(i) may, in the context of this study, be labeled as the proportion of authors with i published articles, and S denotes the summation over i = 1 to 4. Hence the proportion of authors with one article should be:
| f(1) = 1/1(1 + 1) = 0.500. | (4) |
Likewise, the proportions of authors with two, three,..., and i articles should be:
| f(2) = 2(2 + 1) = 0.167, | (5) |
| f(3) = 1/3(3 + 1) = 0.083, | (6) |
and
| f(i) = 1/i(i + 1). | (7) |
Panel D in Table 1 compares actual and predicted proportions of authors with different numbers of articles. The results show that the distribution (3) provides an excellent description of the actual frequency distribution. To test whether the Yule distribution describes the observed data, we perform the Chi-square goodness-of-fit test using the actual and predicted number of authors in Table 1. Since the Chi-square test requires that the predicted (i.e., theoretical) number of observations in each category should be at least five, we used only the relevant sample observations in Table 1 (i.e., the number of articles #) in calculating the Chi-square statistic, Q:
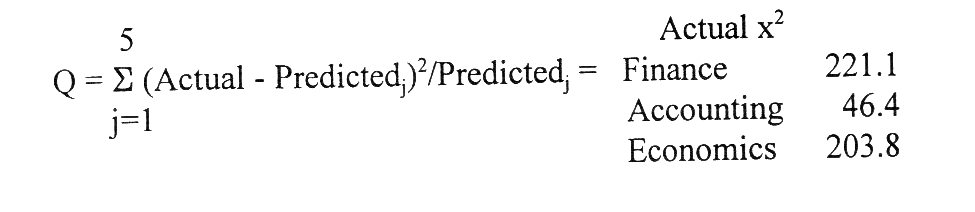 |
Since the Chi-square statistics are greater than x21-2 (K), critical value of 16.75, at the one percent alpha level for finance, accounting and economics, as a whole, respectively, we cannot accept the hypothesis that the Yule distribution with p = 1 represents the process underlying the Superstar phenomenon in the finance, accounting and economics scholarly journal article publication industry. This statistical test shows that the frequency pattern of the Yule distribution, as shown in Panel D of Table 1, is significantly different compared to the actual publishing patterns of the authors displayed in Panels A, B and C in Table 1.
The employment of Equation 7 to test the hypothesis that the Yule distribution represents the stochastic process at the individual journal level provides mixed results. At the extremes the Journal of Financial Economics x2 - statistics of 13.1 supports the superstar phenomenon whereas the Financial Analysts Journal x2 - statistic is 290.6. In the field of accounting there are a number of journals with chi-squared statistics fitting the Yule distribution, especially the Journal of Accounting and Economics with a x2 - statistic of 23.7. The largest x2 - statistic for accounting journals is 137.3 from the Journal of Accounting Education.
The economics journals that lend credence to the existence of the superstar phenomenon are the Brookings Economic Journal (x2 of 18.8) and, again, the Journal of Financial Economics. In contrast, the Review of Economics and Statisticswith a x2 - statistic of 348.9 suggests that there is no such thing as the superstar phenomenon.
AN ALTERNATIVE TEST OF THE YULE DISTRIBUTION
This section presents an alternative test of the Yule distribution as the underlying probability mechanism of the superstar phenomenon. Note first that G(i)/G(i+c).1/ic for any constant c when i is much greater than c [Titchmarsh, 58]. Thus the distribution (1) can be approximated as:
| f(i) =SG(p + 1)i-(p+1) | (8) |
Since f(i) =SG(p + 1)1-(p+1)=SG(p + 1), the distribution (8) can be rewritten as:
| f(i) = f(1)i -(p+1), | (9) |
which upon rearrangement yields:
| f(i)/f(1)=i -(p+1) | (10) |
Finally, taking the log of both sides of (10), we obtain:
| log [f(i)/f(1)]=-(p + 1)log (i). | (11) |
This modified specification of the Yule distribution is tested by applying the following regression model to the frequency distribution data in Table 1:
| log[ f ( i) / f (1) ] = a + B log(i) + e. | (12) |
If the Yule distribution with p. 1 is a reasonable representation of the relative success of authors, we would expect that empirical estimates of the intercept, a, and the slope, B, in (12) should not be significantly different from zero and negative two, respectively. When we apply the above regression model to the empirical frequency distribution in Table 1, we obtain the following results: as displayed in Table 2.
| Finance | Accounting | Economics | |
log [f ( i) / f (1) ] = |
-1.93 |
-1.85 |
-1.87 |
F-value = |
2014 |
913 |
4727 |
The above results show that indeed the Yule distribution is an excellent abstraction of the distribution of the number of articles among different authors in finance, accounting, and economics. It explains nearly 99.8%, 99.6% and 99.8% of the empirical distribution of published articles among authors in finance, accounting, and economics respectively. These overall results for finance, accounting and economics hold at each and every journal. That is, the F-statistic, measuring the explanatory power of Equation 12 which tests for the applicability of the Yule distribution, for each journal is significant at the one percent alpha level. Clearly, the Yule distribution is supported as the stochastic process underlying the superstar phenomenon. This is in contrast to the earlier results reported in Table 1. Nevertheless, it appears the superstar phenomenon does exist at least in the finance, accounting and economics publishing industry.
Furthermore, estimated intercept and slope are not statistically different from zero and negative two, respectively, at the 1% significance level. However, there are some specific journals that do not match this test for additional aspects to the superstar relationship.
Besides the degree of talent, authors have a different amount of resources available to them. Major research universities provide teaching release time, graduate assistant help, cutting edge computers and databases resources to a greater extent compared to teaching universities. The individual author talent must be combined with the level of resources. For example, a symphony violinist sounds better when playing a well-crafted violin as opposed to a shoddy-made violin.
SUMMARY AND CONCLUDING REMARKS
Casual empiricism suggests that there exists a marked skewness in the distribution of output and earnings among individuals in various social-economic fields. Several recent studies have examined this so-called superstar phenomenon, and suggested that much of this phenomenon can be explained by certain consumption technologies and imperfect situations among different sellers. Existing empirical evidence, however, appears to be inconsistent with the prediction of these studies. This paper has examined the phenomenon of superstar from a perspective which is significantly different from that of earlier studies. Specifically, this study views the superstar phenomenon as an implication of the probabilistic mechanism underlying the acceptance of articles for publication behavior of editors. Empirical results suggest that a stochastic process similar to that yielding negative binomial of log series distributions may represent the process generating the superstar phenomenon. Because the scholastic model does not require differential talents levels among individuals, our empirical results suggest that superstar phenomenon could exist among individuals with equal talent. To the extent that very large incomes of superstars are driven by sheer fortune rather than by their superior (if any) talent, the superstar phenomenon may result in a socially inquotable wealth distribution. Thus, when an author compares himself to colleagues with apparently comparable education and experience, yet notes there is a great gulf between the relative success of their careers, he may be observing the superstar phenomenon. The lesser star may console himself knowing that, if only he was a little better, things would have turned out much differently.
Percentage of Authors
Publishing N Articles in a Journal
Panel A
Finance Journals
Frequency Distribution in Percent (N) |
|||||||
| Journal | Number of Authors |
1 |
2 |
3 |
4 |
5 |
>5 |
| FAJ | 1883 |
73.9 |
14.2 |
5.4 |
2.5 |
1.2 |
2.8 |
| FM | 604 |
74.8 |
16.1 |
4.1 |
2 |
1.5 |
1.5 |
| FR | 369 |
79.7 |
14.6 |
3.8 |
1.1 |
0.5 |
0.3 |
| JBR | 426 |
81.5 |
10.8 |
3.5 |
1.9 |
0.9 |
1.4 |
| JBF | 364 |
79.9 |
14.3 |
4.7 |
1.1 |
0 |
0 |
| JBFA | 517 |
75.0 |
.16.9 |
4.4 |
1.4 |
1.5 |
0.8 |
| JF | 1844 |
67.1 |
160 |
7.6 |
3.4 |
2.2 |
3.7 |
| JFE | 297 |
64.3 |
17.2 |
7.4 |
4.4 |
2.7 |
4 |
| JFED | 297 |
79.8 |
13.8 |
3.7 |
1.4 |
1 |
0.3 |
| JFQA | 905 |
68.7 |
17.2 |
7.8 |
2.2 |
1.8 |
2.3 |
| JFR | 306 |
79.0 |
13.1 |
4.9 |
2 |
1 |
0 |
| JFM | 302 |
79.1 |
16.2 |
3 |
0.7 |
0.3 |
0.7 |
| JIMF | 161 |
86.3 |
11.2 |
2.5 |
0 |
0 |
0 |
| JMCB | 685 |
79.6 |
12.3 |
4.9 |
1.8 |
0.7 |
0.7 |
| JPM | 587 |
75.5 |
14.1 |
6 |
2.2 |
1.5 |
0.7 |
| All | 6270 |
62.2 |
15.3 |
.7.1 |
4 |
2.9 |
8.5 |
Source: Heck, Jean Louis and Philip L. Cooley, "Most Frequent Contributors to the Finance Literature," Financial Management, 17 (Autumn 1988), 100-108.
Panel B
Accounting Journals
Frequency Distribution in Percent (N) |
|||||||
Journal |
Number of Authors |
1 |
2 |
3 |
4 |
5 |
>5 |
ABA |
246 |
73.2 |
16.3 |
5.7 |
2.8 |
0.8 |
1.2 |
ABR |
500 |
71.4 |
15 |
5.8 |
3.8 |
1.4 |
2.6 |
AOS |
401 |
72.8 |
16.2 |
4.2 |
3 |
1 |
2.8 |
AR |
1230 |
62.6 |
18.8 |
7.7 |
4.3 |
2.4 |
4.2 |
AJPT |
173 |
75.7 |
17.3 |
4 |
1.7 |
0.6 |
0.7 |
CAR |
129 |
76.7 |
19.4 |
3.1 |
0 |
0.8 |
0 |
IJAER |
434 |
80.6 |
12.9 |
4.4 |
1.2 |
0.9 |
0 |
JAAF |
293 |
84.3 |
10.9 |
3.4 |
0.7 |
0.7 |
0 |
JAE |
132 |
76.5 |
12.9 |
4.5 |
3.8 |
1.5 |
0.8 |
JAED |
291 |
89 |
9.3 |
1.4 |
0.3 |
0 |
0 |
JAL |
83 |
96.4 |
2.4 |
1.2 |
0 |
0 |
0 |
JAPP |
154 |
87.7 |
7.1 |
1.9 |
1.9 |
0.6 |
0.8 |
JAR |
673 |
68.5 |
15.6 |
7.6 |
2.8 |
2.1 |
3.4 |
JBFA |
628 |
69.9 |
17.8 |
6.2 |
2.7 |
0.6 |
2.8 |
All |
3422 |
57.7 |
16.7 |
8.6 |
4.2 |
3 |
9.8 |
Source: Cox, Raymond A.K., and Kee H. Chung, APatterns of Research Output and Author Concentration in the Economics Literature,@ Review of Economics Statistics, 73 (November 1991), 740-747.
Panel C
Economics Journals
Frequency Distribution in Percent (N) |
|||||||
Journal |
Number of Authors |
1 |
2 |
3 |
4 |
5 |
>5 |
AER |
3324 |
67.5 |
16.3 |
6.8 |
3.2 |
2.8 |
3.4 |
JPE |
1743 |
71.3 |
16.8 |
6.4 |
2.5 |
1.3 |
1.7 |
ECA |
1741 |
68 |
16 |
7 |
3.2 |
1.5 |
4.3 |
JME |
651 |
73.4 |
15.1 |
5.2 |
1.8 |
1.2 |
3.3 |
JET |
1005 |
67.9 |
15.9 |
6.9 |
4 |
2.7 |
2.6 |
RSTUD |
1147 |
73.1 |
14.9 |
6 |
3.1 |
1.1 |
1.8 |
IER |
1165 |
75.9 |
13.7 |
5.2 |
3 |
1 |
1.2 |
BJE |
767 |
75.6 |
15.3 |
4.7 |
2.2 |
1.3 |
0.9 |
JF |
1998 |
65.4 |
17 |
6.8 |
3.9 |
2.6 |
4.3 |
JECS |
752 |
71.4 |
14.9 |
6.1 |
2.4 |
2.5 |
2.7 |
SJE |
637 |
78.3 |
11 |
6.3 |
1.3 |
1.4 |
1.7 |
BRK |
241 |
65.6 |
16.2 |
4.1 |
3.3 |
2.5 |
8.3 |
JPUB |
767 |
74.3 |
14.7 |
6.1 |
2.6 |
0.7 |
1.6 |
JFE |
365 |
64.9 |
17.8 |
7.7 |
4.1 |
2.5 |
3 |
RSTAT |
2137 |
73.4 |
18 |
5.2 |
1.6 |
0.9 |
0.9 |
JASA |
1776 |
75.1 |
14.4 |
5.2 |
2.3 |
1.1 |
1.9 |
QJE |
1279 |
77.1 |
15.1 |
5 |
1.5 |
0.6 |
0.7 |
JHR |
807 |
77.4 |
14.5 |
3.3 |
2.7 |
1.4 |
0.7 |
JEL |
287 |
81.5 |
11.5 |
6.3 |
0.3 |
0 |
0.4 |
EJ |
1223 |
73.6 |
17.1 |
5.2 |
2.5 |
0.8 |
0.8 |
All |
13576 |
57.7 |
16.4 |
7.1 |
4.4 |
2.9 |
11.5 |
Source: Chung, Kee Ho, Hong S. Park and Raymond A.K. Cox, "Patterns of Research Output in the Accounting Literature: A Study of Biblio metric Distributions," Abacus, 28 (March 1992), 168-185.
Yule Distribution
Frequency Distribution in Percent
1 |
2 |
3 |
4 |
5 |
>5 |
50 |
16.7 |
8.3 |
5 |
3.3 |
16.7 |
Tests of Yule Distribution
Panel A
Finance Journals
Journal |
(Equation 7) Chi-Square Statistic |
a | (Equation 12) a (t-value) |
B | B (t-value) |
R2 |
F |
t-value (c=2) |
N-size |
| FAJ | 290.6 |
0.059 |
0.66 |
-2.520 |
-31.40 |
1.00 |
986.23 |
6.50 |
5 |
| FM | 104.5 |
0.039 |
0.25 |
-2.541 |
-17.86 |
0.99 |
318.98 |
3.81 |
5 |
| FR | 95.0 |
0.218 |
0.91 |
-3.172 |
-14.80 |
0.98 |
219.08 |
5.48 |
5 |
| JBR | 120.6 |
-0.044 |
-0.56 |
-2.76 |
-39.24 |
1.00 |
1540.15 |
10.86 |
5 |
| JBF | 95.6 |
0.152 |
0.48 |
-2.973 |
-8.99 |
0.96 |
80.75 |
2.94 |
5 |
| JBFA | 92.6 |
0.083 |
0.30 |
-2.639 |
-10.59 |
0.96 |
112.15 |
2.57 |
5 |
| JF | 125.4 |
0.034 |
0.45 |
-2.127 |
-31.45 |
1.00 |
989.23 |
1.87 |
5 |
| JFE | 13.1 |
0.040 |
0.55 |
-1.964 |
-84.51 |
1.00 |
7142.42 |
1.57 |
5 |
| JFED | 74.6 |
0.052 |
0.39 |
-2.822 |
-23.29 |
0.99 |
542.53 |
6.79 |
5 |
| JFQA | 84.7 |
0.118 |
0.52 |
-2.347 |
-11.43 |
0.97 |
130.73 |
1.69 |
5 |
| JFR | 69.2 |
0.049 |
0.60 |
-2.688 |
-36.31 |
1.00 |
1318.43 |
9.30 |
5 |
| JFM | 81.2 |
0.349 |
0.94 |
-3.531 |
-10.56 |
0.97 |
111.42 |
4.58 |
5 |
| JIMF | 65.5 |
0.046 |
0.31 |
-3.194 |
-16.14 |
0.99 |
260.56 |
6.03 |
5 |
| JMCB | 165.4 |
0.097 |
0.52 |
-2.854 |
-17.18 |
0.99 |
295.25 |
5.14 |
5 |
| JPM | 97.2 |
0.029 |
0.27 |
-2.467 |
-25.75 |
0.99 |
662.91 |
4.86 |
5 |
| All | 221.2 |
-0.033 |
-0.69 |
-1.926 |
-44.87 |
1.00 |
2013.54 |
1.72 |
|
Panel B
Accounting Journals
Journal |
(Equation 7) Chi-Square Statistic |
a | (Equation 12) a (t-value) |
B | B (t-value) |
R2 |
F |
t-value (c=2) |
N-size |
| ABA | 35.7 |
.186 |
.64 |
-2.67 |
-10.27 |
.96 |
105.54 |
2.58 |
5 |
| ABR | 57.5 |
.043 |
.25 |
-2.33 |
-14.99 |
.98 |
224.79 |
2.13 |
5 |
| AOS | 59.7 |
.104 |
.46 |
-2.58 |
-12.82 |
.98 |
164.25 |
2.89 |
5 |
| AR | 47.4 |
.080 |
.89 |
-2.01 |
-24.90 |
.99 |
619.99 |
.12 |
5 |
| AJPT | 34.4 |
.239 |
.90 |
-2.98 |
-12.45 |
.98 |
155.07 |
4.10 |
5 |
| CAR | 32.1 |
.156 |
.31 |
-2.82 |
-4.22 |
.89 |
17.84 |
1.23 |
3 |
| IJAER | 113.3 |
.074 |
.40 |
-2.88 |
-17.33 |
.99 |
300.32 |
5.30 |
5 |
| JAAF | 100.3 |
.049 |
.17 |
-3.15 |
-12.12 |
.97 |
146.97 |
4.42 |
5 |
| JAE | 23.7 |
-.069 |
-.35 |
-2.34 |
-13.04 |
.98 |
170.10 |
1.90 |
5 |
| JAED | 137.3 |
.200 |
.62 |
-4.06 |
-12.01 |
.98 |
144.19 |
6.09 |
4 |
| JAL | 57.9 |
-.223 |
-.31 |
-4.14 |
-4.35 |
.90 |
18.91 |
2.25 |
3 |
| JAPP | 66.3 |
-.206 |
-.59 |
-2.95 |
-9.42 |
.96 |
88.78 |
3.04 |
5 |
| JAR | 56.5 |
.039 |
.30 |
-2.20 |
-18.54 |
.99 |
343.62 |
1.68 |
5 |
| JBFA | 74.4 |
.293 |
.69 |
-2.77 |
-7.30 |
.93 |
53.36 |
2.03 |
5 |
| All | 46.4 |
.029 |
.43 |
-1.85 |
-30.22 |
1.00 |
913.29 |
2.46 |
5 |
Panel C
Economics Journals
Journal |
(Equation 7) Chi-Square Statistic |
a | (Equation 12) a (t-value) |
B | B (t-value) |
R2 |
F |
t-value (c=2) |
N-size |
| AER | 237.6 |
-.016 |
-.13 |
-2.06 |
-19.42 |
.99 |
377.15 |
.57 |
5 |
| JPE | 209.4 |
.132 |
.85 |
-2.48 |
-17.84 |
.99 |
318.31 |
3.45 |
5 |
| ECA | 145.8 |
.096 |
.67 |
-2.31 |
-17.96 |
.99 |
322.61 |
2.40 |
5 |
| JME | 102.1 |
.096 |
.68 |
-2.62 |
-20.85 |
.99 |
434.74 |
4.92 |
5 |
| JET | 70.5 |
-.029 |
-.77 |
-2.02 |
-58.48 |
1.00 |
3420.18 |
.59 |
5 |
| RSTUD | 157.5 |
.095 |
.49 |
-2.49 |
-14.17 |
.98 |
200.87 |
2.78 |
5 |
| IER | 204.5 |
.059 |
.31 |
-2.56 |
-14.65 |
.98 |
214.60 |
3.20 |
5 |
| BJE | 135.1 |
.056 |
.78 |
-2.56 |
-39.70 |
1.00 |
1576.25 |
8.75 |
5 |
| JF | 108.6 |
.010 |
.26 |
-2.03 |
-59.19 |
1.00 |
3503.25 |
.88 |
5 |
| JECS | 86.5 |
-.037 |
-.19 |
-2.21 |
-12.78 |
.98 |
163.27 |
1.21 |
5 |
| SJE | 142.1 |
-.021 |
-.07 |
-2.61 |
-9.05 |
.95 |
81.89 |
2.12 |
5 |
| BRK | 18.8 |
-.051 |
-.22 |
-2.13 |
-10.22 |
.96 |
104.41 |
.63 |
5 |
| JPUB | 121.7 |
.182 |
.56 |
-2.73 |
-9.38 |
.96 |
87.91 |
2.51 |
5 |
| JFE | 18.0 |
.047 |
.92 |
-2.02 |
-44.06 |
1.00 |
1940.93 |
.43 |
5 |
| RSTAT | 348.9 |
.218 |
.90 |
-2.79 |
-12.78 |
.98 |
163.38 |
3.61 |
5 |
| JASA | 302.6 |
.076 |
.77 |
-2.59 |
-29.22 |
1.00 |
853.69 |
6.63 |
5 |
| QJE | 266.8 |
.219 |
.82 |
-2.98 |
-12.50 |
.98 |
156.22 |
4.12 |
5 |
| JHR | 165.6 |
-.035 |
-.17 |
-2.51 |
-13.34 |
.98 |
177.99 |
2.71 |
5 |
| JEL | 85.2 |
.325 |
.34 |
-3.59 |
-3.59 |
.80 |
12.87 |
1.59 |
4 |
| EJ | 189.6 |
.197 |
.76 |
-2.72 |
-11.63 |
.97 |
135.37 |
3.09 |
5 |
| All | 203.8 |
.004 |
.14 |
-1.87 |
-68.75 |
1.00 |
4727.00 |
4.81 |
5
|
Appendix A
Journals and Their Abbreviations
Panel A
Finance Journals
Panel B
Accounting Journals
Panel C
Economic Journals
END NOTES
1For a detailed description of this stochastic process, see Simon (1955), pp. 427-433.
2Each of the three studies defined which journals were counted as scholarly and what it took to be classified as an article.
3The tables have abbreviated journal titles. The complete names are in appendix A.
4The time periods covered by these studies are as follows:
REFERENCES
Adler, Moshe. Stardom and Talent. American Economic Review 75 (March 1985): 208-212.
Brown, Lawrence D.. Influential Accounting Articles, Individuals, Ph.D. Granting Institutions and Faculties: A Citation Analysis. Accounting, Organization and Society, 21 (1996): 723-754.
Chung, Kee Ho, Hong S. Park and Raymond A.K. Cox.. Patterns of Research Output in the Accounting Literature: A Study of Biblio metric Distributions. Abacus, 28 (March 1992): 168-185.
Cox, Raymond A.K., and Kee H. Chung. . Patterns of Research Output and Author Concentration in the Economics Literature. Review of Economics and Statistics, 73 (November 1991): 740-747.
Hamlen, William A. Jr. . Superstardom in Popular Music: Empirical Evidence. Review of Economics and Statistics, 73 (November 1991): 729-733.
Heck, Jean Louis and Philip L. Cooley. Most Frequent Contributors to the Finance Literature. Financial Management, 17 (Autumn 1988): 100-108.
Lukka, Kari and Eero Kasanen. Is Accounting a Global or a Local Discipline? Evidence from Major Research Journals. Accounting, Organization and Society, 21 (1996): 755-773.
MacDonald, Glenn M. The Economics of Rising Stars. American Economic Review, 78 (March 1988): 155-167.
Rosen, Sherwin. The Economics of Superstars. American Economic Review, 71 (December 1981):
845-858.
Simon, Herbert A. On a Class of Skew Distribution Functions. Biometrika, 42 (1955): 425-440.
Titchmarsh, E.C. The Theory of Functions. London: Oxford University Press, 1939.
Yule, G. Udny. A Mathematical Theory of Evolution, based on the Conclusions of Dr. J.C. Willis, F.R.S. Philosophical Transactions of the Royal Society, B. 213 (1924): 21-87.
Willis, F. R. S. Philosophical Transactions of the Royal Society, B. 213 (1924): 21-87.
